Maximum common subgraph
Maximum common subgraph (MCS) is considered as one of the most challenging problems in
combinatorial optimization. As a generalization to (sub-) graph isomorphism, MCS has deep roots within cheminformatics. From reaction mapping to enabling molecular graphs as first-class objects in kernel-based QSAR methods, MCS has become a basic necessity in any cheminformatics toolbox. However, the utility of MCS (or lack thereof) is currently limited by our inability to solve MCS efficiently. Pending a significant development in computational complexity theory, this fact will likely to remain true for a forseeable future.
Despite the inherent "hardness" in solving MCS, there exist a number of algorithms for solving MCS within reasonable time on modern hardware. For a good survey of MCS algorithms, please see this
paper. The purpose of this post, as such, is to briefly describe our approach to solving MCS and, more generally, to the problem of solving MCS for a set of molecular graphs. Multiple MCS (as the latter problem is often known) has numerous applications in cheminformatics such as Markush structure extraction (e.g., see our related
R-group decomposition tool), generalizing bioisostere replacement beyond pairwise, (2D) pharmacophore elucidation, and so forth.
Clique-based approaches are arguably the current state-of-the-art for solving exact MCS. Here the MCS problem is transformed into one of finding the
maximum clique of the corresponding
association graph. This approach has a number of desired properties including (but are not limited to) the following:
- Algorithmic elegance. The clique finding problem has been well-studied in computer science, so there exist many well-known algorithms available (e.g., see the second DIMACS implementation challenge). Most of the published maximum clique algorithms are quite easy to understand. In fact, the most problematic aspects of the clique-based approach, in terms of code, are likely to be in the construction of the association graph and bounding function. The actual clique finding routine can be expressed in a few lines of code using any modern computer programming language.
- Optimized implementation. Since most efficient clique solvers are based on the branch-and-bound algorithm, they can easily be parallelizable on modern multi-core CPUs. Moreover, with some care the implementation of a clique solver can be done entirely with bit twiddling.
- Built-in support for disconnected MCS. Due to the nature of the association graph, the resulting maximum clique often yields disconnected MCS's. This can be quite useful, for example, in the identification and visualization of bioisostere replacements.
Notwithstanding these properties, however, clique-based approaches have a few drawbacks. Given two graphs
G1 and
G2 with
m and
n nodes, respectively, the number of nodes in the corresponding association graph is in the order of
mn. Even with a modest sized molecule of 20 atoms, this can result in an association graph of 400 nodes. Here a fast clique solver will likely to spend a few CPU seconds finding the maximum clique.
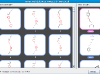
Thus far we've considered MCS as an optimization problem, the premise being that the best solution is also the right one. This is certainly true for most general cases, but for cheminformatics it's not quite so obvious. Consider, for example, the following two molecules:

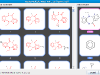
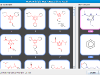
There are at least 26 different maximum subgraph isomorphisms here. Let's look at one specific MCS below

The numbering denotes isomorphisms between the two molecules. (This example also highlights the fact that we only consider maximum common edge subgraph isomorphism.) Depending on the context, the MCS above might be desirable in that it captures the carboxyl functional group. In other context, it might be the case that the less optimal subgraph isomorphism corresponds to the indole scaffold is desirable.

To remedy this shortcoming, a different approach is to consider MCS as a clique enumeration problem. That is, instead of finding the maximum clique, we enumerate all maximal cliques in the association graph. Each maximal clique, in turn, corresponds to a subgraph ismorphism, which may or may not be the actual MCS. The distinction between this approach and that of the maximum clique is effectively there are no bounds defined, so the entire search space is evaluated. Given there can be as much as
3(n/3) cliques in a graph of
n nodes, such exhaustive enumeration can be prohibitly expensive.
An effective strategy to speed up the enumeration is to reduce the size of the association graph. This is precisely the approach behind the
C-clique algorithm (and also
improvements thereof). By considering only connected subgraph ismorphomism, the C-clique algorithm significantly reduces the size of the search space, thereby making it a very effective algorithm for MCS. This is the algorithm that motivates our fragment-based (multiple) MCS approach, which we briefly discuss below. (For the impatient, please click
here to take the multiple MCS tool for a spin.)
The main idea behind our fragment-based approach, as we
hinted at previously, is to simply use fragments as seeds to the C-clique algorithm. Effectively, this seeding serves to (i) further reduce the search space, (ii) focus the search in a specific direction, and (iii) move a good portion of the burden in dealing with internal symmetry of the MCS out of C-clique. This last point is significant in that it allows us to use other algorithms that are much more effective for automorphism detection. (Clique-based MCS algorithms are notoriously bad in dealing with symmetry.)
Multiple MCS is simply an extension to the fragment-based MCS. Here an advantage to our fragment-based approach is that we know, given a set of molecules, the fragments that span the entire set (if any). This allows us to do pairwise MCS with appropriately seeded fragments to eventually arrive at the multiple MCS. Clearly, pairwise MCS without seeded fragments will likely yield a non-optimal solution (if any at all).
The tool to try out multiple MCS is available
here. We believe the algorithm is fundamentally correct. Any unexpected result is likely due to bugs in our implementation, in which case we'd love to hear about it.
 Maximum common subgraph (MCS) is considered as one of the most challenging problems in combinatorial optimization. As a generalization to (sub-) graph isomorphism, MCS has deep roots within cheminformatics. From reaction mapping to enabling molecular graphs as first-class objects in kernel-based QSAR methods, MCS has become a basic necessity in any cheminformatics toolbox. However, the utility of MCS (or lack thereof) is currently limited by our inability to solve MCS efficiently. Pending a significant development in computational complexity theory, this fact will likely to remain true for a forseeable future.
Despite the inherent "hardness" in solving MCS, there exist a number of algorithms for solving MCS within reasonable time on modern hardware. For a good survey of MCS algorithms, please see this paper. The purpose of this post, as such, is to briefly describe our approach to solving MCS and, more generally, to the problem of solving MCS for a set of molecular graphs. Multiple MCS (as the latter problem is often known) has numerous applications in cheminformatics such as Markush structure extraction (e.g., see our related R-group decomposition tool), generalizing bioisostere replacement beyond pairwise, (2D) pharmacophore elucidation, and so forth.
Clique-based approaches are arguably the current state-of-the-art for solving exact MCS. Here the MCS problem is transformed into one of finding the maximum clique of the corresponding association graph. This approach has a number of desired properties including (but are not limited to) the following:
Maximum common subgraph (MCS) is considered as one of the most challenging problems in combinatorial optimization. As a generalization to (sub-) graph isomorphism, MCS has deep roots within cheminformatics. From reaction mapping to enabling molecular graphs as first-class objects in kernel-based QSAR methods, MCS has become a basic necessity in any cheminformatics toolbox. However, the utility of MCS (or lack thereof) is currently limited by our inability to solve MCS efficiently. Pending a significant development in computational complexity theory, this fact will likely to remain true for a forseeable future.
Despite the inherent "hardness" in solving MCS, there exist a number of algorithms for solving MCS within reasonable time on modern hardware. For a good survey of MCS algorithms, please see this paper. The purpose of this post, as such, is to briefly describe our approach to solving MCS and, more generally, to the problem of solving MCS for a set of molecular graphs. Multiple MCS (as the latter problem is often known) has numerous applications in cheminformatics such as Markush structure extraction (e.g., see our related R-group decomposition tool), generalizing bioisostere replacement beyond pairwise, (2D) pharmacophore elucidation, and so forth.
Clique-based approaches are arguably the current state-of-the-art for solving exact MCS. Here the MCS problem is transformed into one of finding the maximum clique of the corresponding association graph. This approach has a number of desired properties including (but are not limited to) the following:
 There are at least 26 different maximum subgraph isomorphisms here. Let's look at one specific MCS below
There are at least 26 different maximum subgraph isomorphisms here. Let's look at one specific MCS below
 The numbering denotes isomorphisms between the two molecules. (This example also highlights the fact that we only consider maximum common edge subgraph isomorphism.) Depending on the context, the MCS above might be desirable in that it captures the carboxyl functional group. In other context, it might be the case that the less optimal subgraph isomorphism corresponds to the indole scaffold is desirable.
The numbering denotes isomorphisms between the two molecules. (This example also highlights the fact that we only consider maximum common edge subgraph isomorphism.) Depending on the context, the MCS above might be desirable in that it captures the carboxyl functional group. In other context, it might be the case that the less optimal subgraph isomorphism corresponds to the indole scaffold is desirable.
 To remedy this shortcoming, a different approach is to consider MCS as a clique enumeration problem. That is, instead of finding the maximum clique, we enumerate all maximal cliques in the association graph. Each maximal clique, in turn, corresponds to a subgraph ismorphism, which may or may not be the actual MCS. The distinction between this approach and that of the maximum clique is effectively there are no bounds defined, so the entire search space is evaluated. Given there can be as much as 3(n/3) cliques in a graph of n nodes, such exhaustive enumeration can be prohibitly expensive.
An effective strategy to speed up the enumeration is to reduce the size of the association graph. This is precisely the approach behind the C-clique algorithm (and also improvements thereof). By considering only connected subgraph ismorphomism, the C-clique algorithm significantly reduces the size of the search space, thereby making it a very effective algorithm for MCS. This is the algorithm that motivates our fragment-based (multiple) MCS approach, which we briefly discuss below. (For the impatient, please click here to take the multiple MCS tool for a spin.)
The main idea behind our fragment-based approach, as we hinted at previously, is to simply use fragments as seeds to the C-clique algorithm. Effectively, this seeding serves to (i) further reduce the search space, (ii) focus the search in a specific direction, and (iii) move a good portion of the burden in dealing with internal symmetry of the MCS out of C-clique. This last point is significant in that it allows us to use other algorithms that are much more effective for automorphism detection. (Clique-based MCS algorithms are notoriously bad in dealing with symmetry.)
Multiple MCS is simply an extension to the fragment-based MCS. Here an advantage to our fragment-based approach is that we know, given a set of molecules, the fragments that span the entire set (if any). This allows us to do pairwise MCS with appropriately seeded fragments to eventually arrive at the multiple MCS. Clearly, pairwise MCS without seeded fragments will likely yield a non-optimal solution (if any at all).
The tool to try out multiple MCS is available here. We believe the algorithm is fundamentally correct. Any unexpected result is likely due to bugs in our implementation, in which case we'd love to hear about it.
To remedy this shortcoming, a different approach is to consider MCS as a clique enumeration problem. That is, instead of finding the maximum clique, we enumerate all maximal cliques in the association graph. Each maximal clique, in turn, corresponds to a subgraph ismorphism, which may or may not be the actual MCS. The distinction between this approach and that of the maximum clique is effectively there are no bounds defined, so the entire search space is evaluated. Given there can be as much as 3(n/3) cliques in a graph of n nodes, such exhaustive enumeration can be prohibitly expensive.
An effective strategy to speed up the enumeration is to reduce the size of the association graph. This is precisely the approach behind the C-clique algorithm (and also improvements thereof). By considering only connected subgraph ismorphomism, the C-clique algorithm significantly reduces the size of the search space, thereby making it a very effective algorithm for MCS. This is the algorithm that motivates our fragment-based (multiple) MCS approach, which we briefly discuss below. (For the impatient, please click here to take the multiple MCS tool for a spin.)
The main idea behind our fragment-based approach, as we hinted at previously, is to simply use fragments as seeds to the C-clique algorithm. Effectively, this seeding serves to (i) further reduce the search space, (ii) focus the search in a specific direction, and (iii) move a good portion of the burden in dealing with internal symmetry of the MCS out of C-clique. This last point is significant in that it allows us to use other algorithms that are much more effective for automorphism detection. (Clique-based MCS algorithms are notoriously bad in dealing with symmetry.)
Multiple MCS is simply an extension to the fragment-based MCS. Here an advantage to our fragment-based approach is that we know, given a set of molecules, the fragments that span the entire set (if any). This allows us to do pairwise MCS with appropriately seeded fragments to eventually arrive at the multiple MCS. Clearly, pairwise MCS without seeded fragments will likely yield a non-optimal solution (if any at all).
The tool to try out multiple MCS is available here. We believe the algorithm is fundamentally correct. Any unexpected result is likely due to bugs in our implementation, in which case we'd love to hear about it.